NUMEROS ENTEROS

CONJUNTO DE NÚMEROS ENTEROS 

NÚMEROS ENTEROS:

El conjunto de los números enteros se considera como la unión del conjunto de números enteros negativos, el conjunto de enteros positivos y el cero.

REPRESENTACIÓN EN LA RECTA NUMÉRICA: 
todos los elementos del conjunto de números enteros se pueden representar gráficamente en la recta numérica en la siguiente manera

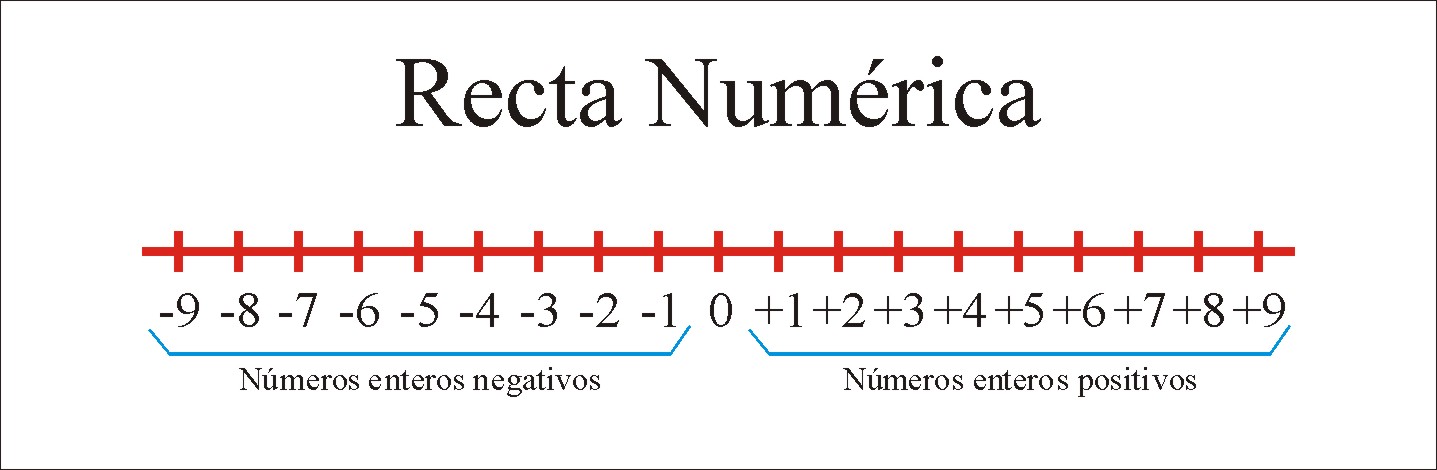
REPRESENTACIÓN EN EL PLANO CARTESIANO 

el plano cartesiano se reconoce los siguientes elementos:
*la recta numérica horizontal denominada eje x  y la recta numérica denominada eje y.
*el punto de intersección, llamado origen.
*las 4 regiones generadas por dos ejes que dividen al plano son denominada cuadrante y se representan con los números romanos 1 2 3 y 4.

ejemplo:

VALOR ABSOLUTO DE UN NUMERO ENTERO
el valor absoluto de un numero entero corresponde a la distancia de un numero respecto al cero.

si a es un numero entero, el valor absoluto de a se nota |a| => valor absoluto de a y es la distancia que hay entre a y el cero. el valor absoluto de cero es cero.
Ejemplos: calcular el valor absoluto en cada caso.
a.|6|

b.|-9|                x, si x > 0

c.|10|                0, si x = 0

d.|x|                 x, si x < 0

ORDEN EN LOS NUMEROS ENTEROS
al comparar 2 números enteros a y b entre ellos se cumple una y solo una de las siguientes relaciones:

EJEMPLO: observar la recta numérica. luego, escribir los símbolos mayor, ><, =, para relacionarlas siguientes parejas de números.
a.6 > 5
b-3 < -10 

c.-5 < 8

ejemplo:
2.representar los números  ordenarlos de menor a mayor. , -10, 4, 6, -8, -5, 1, -3.
                                  -10< -8 < -5 < -3 <1 <4 <6
OPERACIONES EN LOS NÚMEROS ENTEROS :suma:en la suma de números enteros se debe tener en cuenta los siguientes casos:
caso 1: suma de dos números de igual signo.

para realizar la suma de dos números enteros de igual signo.
se suman los valores absoluto de dicho numero se le ante pone el signo común de los humanos por ejemplo:   3+5=|5| =8
                 (-7) + (-4) = |-7| + |-4| = - ( 7 + 4 ) = - 11
PROPIEDADES DE LA SUMA DE NUMEROS ENTEROS:
para la adición, los números enteros cumplen las siguientes propiedades.
1. propiedad clausurara: la suma de dos números  enteros es otro numero entero.
                       a,b EZ, entonces, a + b EZ
por ejemplo, 3 es un numero entero
P. E: (-3) EZ, -2 EZ, (-3+(-2)= 1 EZ
PROPIEDAD ASOCIATIVA 
al agruparlos los comando de diferentes formas, siempre se obtiene el mismo resultado.
            Si a, b, c, son numeros enteros, entonces,
p. Asociativa: a, b, c EZ, ent, (a+b) + c = a + (b+c) = ( a + c )+ b
P.E: (-7+3) + a = -7 + (3+9) + 9 = (9-7)+3=9(-7+3)
                      5=5=5=5=5
PROPIEDAD CONMUTATIVDA: 
el orden en que se realice la suma de dos números enteros, no afecta el resultado.
P. comutativa 

si a,b EZ, ent,
P. E: 5+(-2) = (-2)+5
5-2 = - 2 + 5
      3=3
PROPIEDADES NEUTRO: 
 la suma de cualquier numero entero con el 0, da como resultado el mismo numero. el 0 recibe el nombre elemento neutro o modulo para la suma.
a EZ, ent, a +0 = a 
-5+0=5 ros 
3+0=3
INVERSO ADICTIVO U OPUESTO: 
Todo numero entero sumado con sub opuesto o inverso adictivo da como resultado el modulo para la suma

si a, -a EZ, y -a es el opuesto de a ,ent, a+ (-a)=0
P.E. 3+(-3) = 3-3= 0
 EJEMPLO:   De una deporadora de agua que continental 4.500 L de agua, se sacaron 2.500 L después se depositaron 4.000 L y por ultimo se sacaron 6.000 L ¿cuantos litros de agua contiene ahora la deporadora.  

[4.500+(-2.500)+[4.000]+(-600)]

    -2000+(-2.000)

             0 

SUPRESIÓN DE SIGNOS DE AGRUPACIÓN .

En expresiones en las cuales se combinan adiciones y sustracciones con números con enteros,se utilizan signos de agrupación con el fin de diferenciar el signo de números respeto   al signo de la operación. por ejemplo.

P.E: (-3)+2+(-5)+(-4)

para resolver se debe eliminar los signos de agrupación teniendo en cuenta las  siguientes reglas:

*cuando un signo de agrupación  esta presidido por el signo mas, suprime las cantidades con el mismo signo, así.
    5+(-2) = 5-2 = 3

cuando un signo de agrupación esta presidido por el signo menos, se suprime cambiando de signo las cantidades que se encuentran en el interior, es decir,
         5-(-3) = 5+3 =8
         -6-(3+2-5-7+9)
          6+3-2+5+7-9
                22-11

                   11
ejemplos:
a). (-10)-(-15) -10+15=15-10=5
b). (-14)+(-3)-(-8)
 -14-3+8
   -17+8
      -9
c).(-11)+(-6)-(-4)-(-1)
         -11-6+4+1
           -17+5
            -12 

POTENCIACION DE NÚMEROS ENTEROSla potenciacion se define como en la operacion que  simplifica de varios factores igual, es decir, si E Z y n E Z, ent,axaxaxa... x a =an              n-veces
ejemplo:(-2)4 = 16 →potencial
 (-2)4=(-2)x(-2)x(-2)x(-2) = 16
*si la base es negativa y el exponente es par la potencia es positiva. por ejemplo:
(-3)2=(-3) (-3) =9
* si la base es negativa y el exponente es impar, la potencia es negativa.
(-3)3=(-3) (-3) (-3) = - 27
* si la base es positiva y el exponente es par o impar, la potencia es positiva:
por ejemplo:24= 2 x 2 x 2 x 2= 16
                      25 = 2 x 2 x 2 x 2 x 2 = 32
propiedades de la potenciacion 
la potenciacion de números enteros cumple las siguientes propiedades:
*producto de potencialisacion  de igual base:
*para multiplicar potencia de igual base y condiferente exponente, se deja la misma base y se suman los exponentes.
es decir, si a E Z Y n, m E N, ent, an x am = an+m
ejemplo: 35x32=33+5 =37
* cosiente de potencia de igual base. para dividir potencia de igual base y diferente exponente, se deja la misma base y se resta los exponentes.
es decir, si a es un numero ent, an : am  = an+ m y a distinto de cero a y n mayor que m=n>m

                             POTENCIA DE UNA POTENCIA

Es otra potencia con la misma base y cuyo exponente es el producto de los exponentes.

      (a^m)ⁿ = a^{m · n}

Ejemplo:

[(−2)³]² = (−2)⁶ = 64

POTENCIA DE UN PRODUCTO para calcular la potencia de un producto, se eleva cada factor de producto a exponente indicado.
es decir, sia y b son numeros enteros y n, es un numero natural, ent, (axb)n = anxbn
ejemplos: ((-3)x4)elevado a la 2 =9 x 16 = 144 

POTENCIA DE UN COCIENTE:  

para calcular la potencia de un cociente, se elabora cada uno de los elementos de la división, es decir, si a y b son numeros enteros y n es numero natura, etc, 

(a:b)n= an : bn

por ejemplo: (3/5)elevado a la 4 = 34 / 54  

.